벨만포드(Bellman-Ford) 알고리즘
벨만포드 알고리즘은 하나의 정점에서 출발해 다른 모든 정점까지의 최단거리를 구하는 알고리즘이다. 다익스트라 알고리즘과 달리, 가중치가 음수일 때도 동작하며, 음의 사이클의 존재 여부도 탐지할 수 있다.
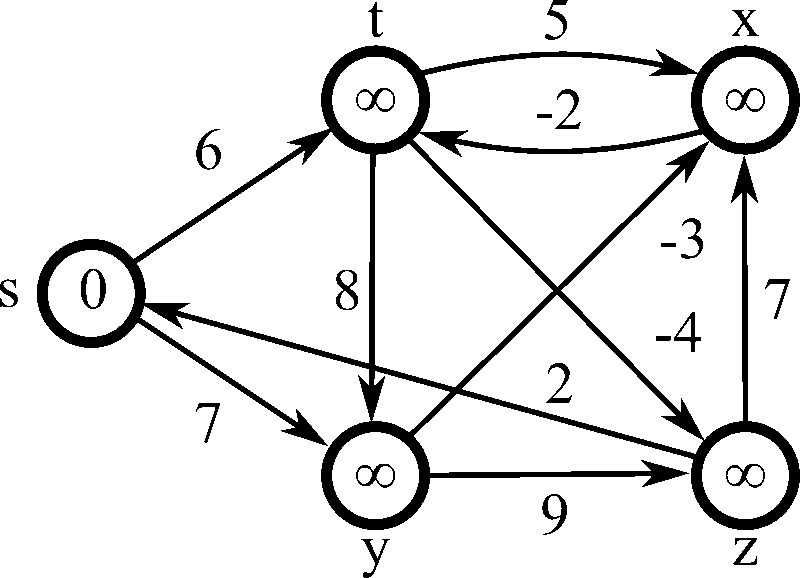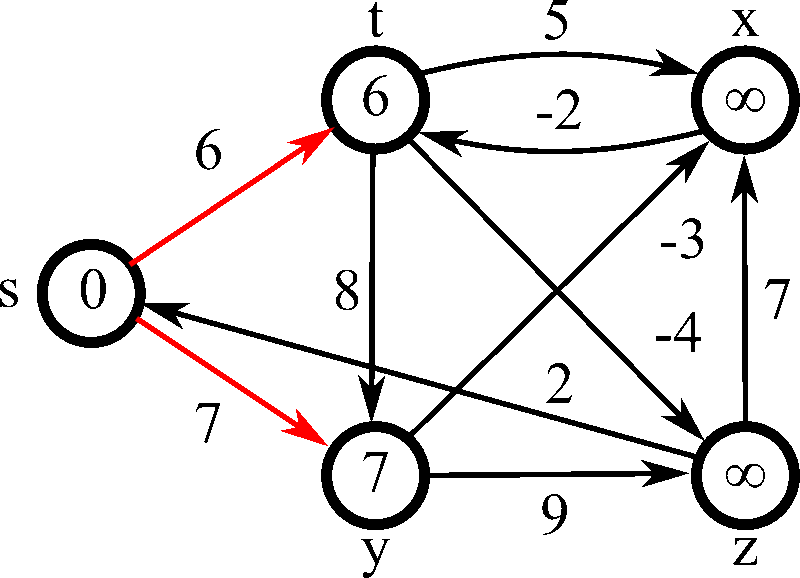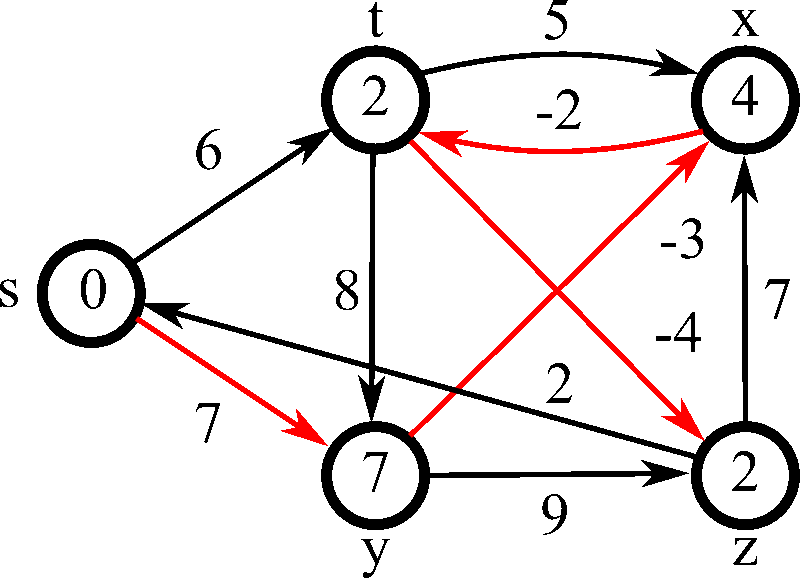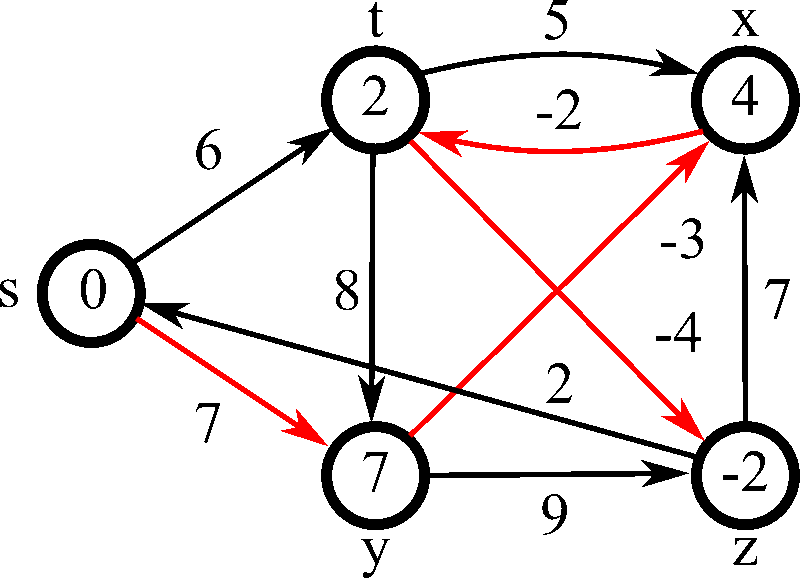출처: 위키피디아
벨만포드 알고리즘을 잘 설명해주는 gif인 것 같다.
🧠 과정
d 리스트에는 출발점으로부터 각 노드까지의 최단 거리가 저장된다.
- 모든 노드의 거리를 무한대(
inf)로 초기화하고, 시작 노드의 인덱스(노드 번호)만 0으로 설정한다. - 모든 노드들을 번호 순서대로 확인하되, 현재 확인 중인 노드의 최단거리가
inf가 아닌 경우에 한해, 그 노드 A와 연결된 모든 노드 B에 대해d[A] + (A와 B 사이의 거리)가d[B]보다 작으면d[B]를 갱신한다. - 2번 과정을
(노드의 개수 - 1)번 반복한다. - 알고리즘을 종료한다. 단, 음의 사이클이 있는지 확인하고 싶다면 2번 과정을 한 번 더 수행해
d에 변화가 있는지 확인한다.
VS 다익스트라 알고리즘
공통점
두 알고리즘 모두 d 리스트에 각 노드의 최단 거리를 저장하고, 계산이 끝난 뒤에 d[목적지 노드번호]를 확인해 최단 거리를 알 수 있다는 점에서 동일했다.
차이점
다익스트라는 매번, 아직 방문하지 않은 노드 중에서 최단거리가 짧은 노드를 선택한다(리스트 순회 or 우선순위 큐 사용).
반면, 벨만포드는 노드의 방문 여부와 상관없이, 각 노드와 이어진 모든 노드들을 매번 전부 방문하면서 최단거리를 갱신한다.
즉 벨만포드는 단순하다.
모든 간선을 본다.
또 모든 간선을 본다.
또또 모든 간선을 본다.
그렇게 (정점 개수) - 1 번 반복한다.
그래프 전체의 모든 간선(E개, 동떨어져있는 간선들의 경우 제외긴 하다)을 노드의 개수(V번)만큼 반복하기 때문에, 벨만포드의 시간 복잡도는 O(VE)다.
다익스트라: O(ElogV)
벨만포드: O(VE)
시간복잡도만 놓고 보면 다익스트라가 훨씬 빠르지만, 다익스트라는 음수 간선이 있으면 해를 구할 수 없다. 왜냐하면, 다익스트라는 시작 노드에서 가장 가까운 노드부터 차례차례 최단거리를 확정해나가는 구조다. 한 번 방문된 노드는 더이상 갱신되지 않는다는 전제 하에 그리디하게 돌아가는 게 가능하다.
하지만 음수 간선이 존재한다면, 이미 방문했던 노드라도 나중에 더 짧은 경로로 다시 갱신될 수 있다. 즉, 다익스트라의 ‘확정’ 구조가 불가능하다.
이 때문에 벨만포드는 방문 여부에 관계없이 모든 간선을 계속 반복적으로 확인해야 하고, 그래서 느리다…
결론
- 모든 가중치가 양수라면 다익스트라를 쓰는 것이 낫다.
- 음수 간선이 있을 가능성이 있다면 벨만포드를 써야 한다.
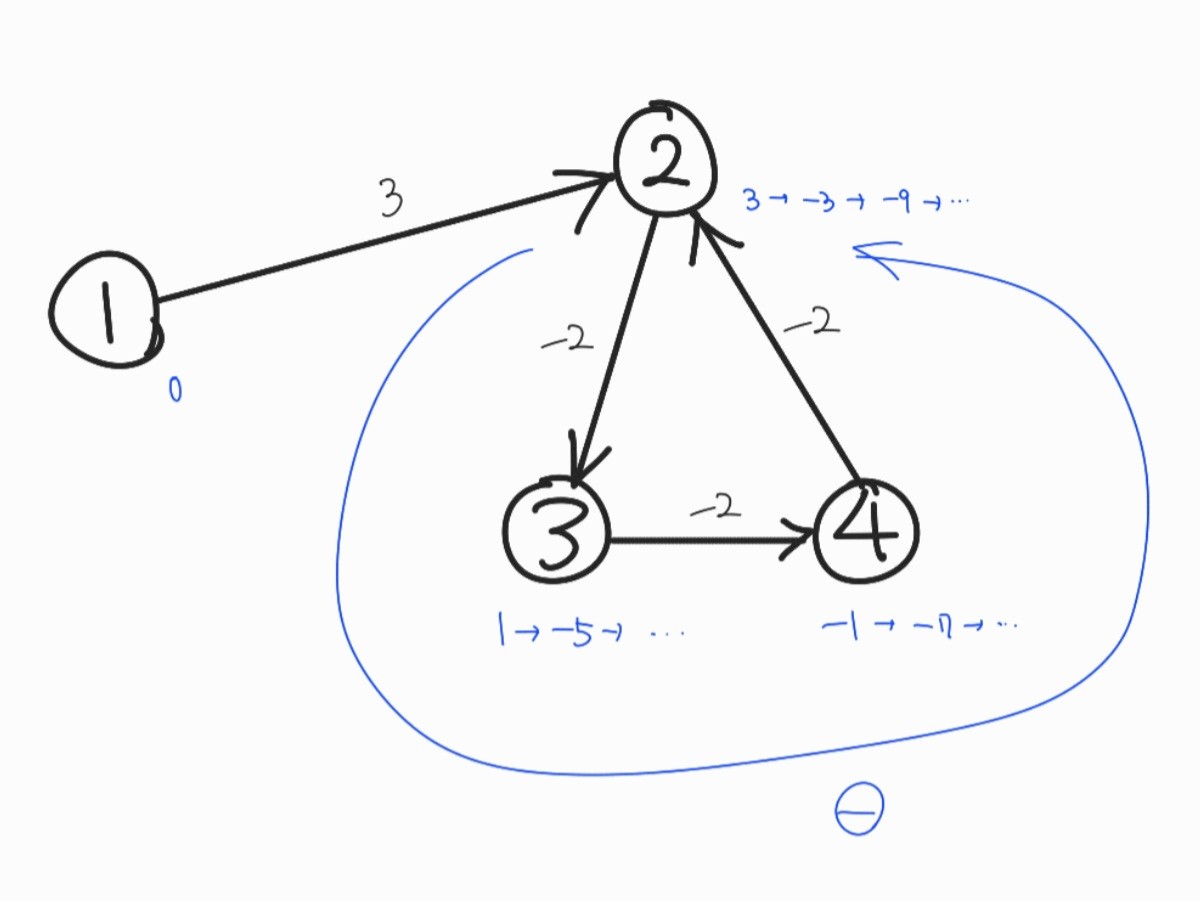
👻 음수 간선 순환(음의 사이클)
음의 사이클: 돌고 돌수록 거리가 짧아지는 매직
벨만포드는 음의 사이클 존재 여부를 판별할 수 있다.
출발 노드에서 다른 노드까지의 최단경로를 위해 지나는 간선의 개수는 최대 V-1개일 수밖에 없다. 그러니, V-1번째 반복을 끝내고 마지막 V번째 반복을 할 때, 이때도 갱신되는 값이 있다면 음의 사이클이 존재한다는 뜻이다.
문제
음의 사이클이 존재하는지 판단하는 문제다.
❌ 틀린 코드와 이유
어차피 V번째 반복만 확인하면 되니, 아무 정점에서나 출발해도 될 거라고 생각했다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import copy
import sys
input = sys.stdin.readline
TC = int(input())
for _ in range(TC):
N, M, W = map(int, input().split())
# 각 정점의 최단거리 정보
d = [float('inf') for _ in range(N + 1)]
d[0] = 0
d[1] = 0 # 1번 노드에서 출발(임의로 그렇게 정함)
# 각 정점과 연결된 간선들 정보
edges = [[] for _ in range(N + 1)]
# 간선 정보 입력받기
for _ in range(M):
S, E, T = map(int, input().split())
edges[S].append((E, T))
for _ in range(W):
S, E, T = map(int, input().split())
edges[S].append((E, -T))
# N-1번째 반복을 마쳤을 때의 d의 상태를 저장할 리스트
tmp_d = []
# 벨만포드 알고리즘
for i in range(1, N+1):
# 최단거리가 무한대가 아닌 노드들 번호 골라내기
these_nodes = []
for node_num in range(1, N+1):
these_nodes.append(node_num) if d[node_num] != float('inf') else None
# 해당 노드들과 연결된 노드들의 최단거리 갱신
for start_num in these_nodes:
for edge in edges[start_num]:
end_num = edge[0]
weight = edge[1]
if d[start_num] + weight < d[end_num]:
d[end_num] = d[start_num] + weight
# N-1번째 반복을 마쳤을 때의 d의 상태 저장: 리스트 깊은복사 필요
if i == N-1:
tmp_d = copy.deepcopy(d)
# 음수 사이클이 존재하는지 여부
negative_flag = tmp_d != d
# 출력
print('YES' if negative_flag else 'NO')
틀렸습니다를 받았다. 위 코드는 임의로 1번에서만 출발하는데, 만약 음의 사이클이 1번 노드와 동떨어진 곳에 존재한다면 이걸 탐지해낼 수 없어 오답 판정을 받게 된다.
그럼 모든 정점에서 한번씩 출발하도록 이 과정을 V번 반복해야 하나?
그럼 O(EV)를 V번? …
➡️ 정답은 모든 정점의 최단거리를 0으로 초기화하는 것이었다.
이 방법은 각 정점까지의 정확한 최단거리를 구하지는 못하지만, 이 문제는 음의 사이클 유무만 확인하면 되는 문제이기 때문에 d 리스트에 어떤 값이 들어있냐와 관계없이 오직 V번째 반복에서 갱신이 발생했는지만 보면 된다.
모든 정점의 거리를 0으로 시작한다는 파격적인 선택(?)이, 최단거리 계산에만 영향을 주고, 음의 사이클 탐지에는 전혀 영향을 안 준다는 점이 기억에 남는다.
✅ 정답 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import copy
import sys
input = sys.stdin.readline
TC = int(input())
for _ in range(TC):
N, M, W = map(int, input().split())
# 각 정점의 최단거리 정보
d = [0 for _ in range(N + 1)]
# 각 정점과 연결된 간선들 정보
edges = [[] for _ in range(N + 1)]
# 간선 정보 입력받기
for _ in range(M):
S, E, T = map(int, input().split())
edges[S].append((E, T))
edges[E].append((S, T))
for _ in range(W):
S, E, T = map(int, input().split())
edges[S].append((E, -T))
negative_flag = False
tmp_d = []
# 벨만포드 알고리즘
for i in range(1, N+1):
# 해당 노드들과 연결된 노드들의 최단거리 갱신
for start_num in range(1, N+1):
for edge in edges[start_num]:
end_num = edge[0]
weight = edge[1]
if d[end_num] > d[start_num] + weight:
d[end_num] = d[start_num] + weight
# N-1번째 반복이라면 d의 상태 저장: 리스트 깊은 복사
if i == N-1:
tmp_d = copy.deepcopy(d)
# 음수 사이클이 존재하는지 여부
negative_flag = d != tmp_d
# 출력
print('YES' if negative_flag else 'NO')
+) 이 문제는 플로이드-워셜로도 풀 수 있다고 한다. 다음에 도전해보자!